
Application Studies using the
3DOPT Integrated Design System©
William W. Herling*, Stephen T. LeDoux†, Robert R. Ratcliff†,
Boeing Information, Space & Defense Systems,
Seattle, Washington
Abstract
An application of the 3-Dimensional Design Optimization
Code, 3DOPT, has been performed and compared with previous optimization
results, in addition to recent direct driven optimization results. This
paper discusses these results and examines several refinement strategies
for enhancing the 3DOPT design of experiments models. Results presented
will show that 3DOPT has provided additional areas of improvement within
the global design space. This work represents the first application of
the 3DOPT system for a design optimization study.
Introduction
The reduction of design cycle time is a current area of interest for both the design of commercial and military flight hardware. The desire to meet this challenge while at the same time meet growing design performance demands, has motivated the development of design optimization tools in general and aerodynamic design optimization tools in particular. The aerodynamic design tools can be divided into two general categories, direct driven and approximate modeling. With the former, all information required by a given optimization search algorithm is provided directly by a cost function evaluator while with the latter the optimization search is performed with an approximate model of the design space. The approximate model is created using one of a variety of surface fitting techniques based on a population of cost function values determined at a specified number of locations distributed through the multi-dimensional design space.
Within both categories local and global optimization search schemes have been devised. Each of these approaches carries with them a characterizing set of advantages and disadvantages. In general terms, the local techniques tend to be more precise in identifying an optimal, although local, condition while the global techniques tend to be more probabilistic in nature and require more function evaluations. Furthermore, the local techniques tend to be integrated into direct driven frameworks while the global techniques, at least for expensive cost function evaluations, tend to be integrated into approximate model frameworks.
This leads to a question of performance trade-off
between the two approaches. In a manufacturing design environment the issue
is not global versus local optima. Many successful design optimization
applications have been achieved within Boeing using local optimization
search algorithms. The question is what is the performance of the design,
does it meet constraints and how much does it cost, or how long does it
take? This paper examines this question within the context of three different
optimization approaches for a simple, but representative, aerodynamic design
problem.
Description of Optimization Approaches
The optimization approaches used were 3DOPT
(Ref. 1,2,3, a global approximate modeling approach),
TRANAIR Design (Ref. 4, a local approximate modeling
approach), and a local direct driven version of 3DOPT. The 3DOPT program
is an optimization system that will perform wing alone, or wing in the
presence of a body, optimizations using potential flow, Euler or Navier-Stokes
level physics. Geometry input options are available that are connected
to a library of geometric perturbations controlling details of airfoil
section design and wing planform characteristics. Design space characteristics
are modeled using interpolated response surfaces from which global optimization
searches are performed. An overview of the 3DOPT system is illustrated
in Figure 1. The main components of the system, and the process steps in
a design space search with 3DOPT are shown. The major technology components
of the system are the David Taylor Non-Uniform Rational B-Spline (DT_NURBS,
Ref.
5) geometry library, design and analysis of computer experiments (DACE,
Ref. 6) technology library, HYPGEN (Ref.
7) hyperbolic volume grid generator , TLNS3D (Ref.
8) Euler/Navier-Stokes flow solver, TWING (Ref. 9)
full potential flow solver, NPSOL (Ref. 10) gradient
based nonlinear, constrained optimization search program, and BGENETIC
hybrid genetic/gradient optimization search program.

TRANAIR is based on Newton’s method for the solution of the full potential fluid dynamic equations with a coupled strip boundary layer. Solution adaptive local grid refinement supports the analysis of complex three-dimensional geometries. The design optimization capability makes use of transpiration boundary conditions to model surface geometry changes and a linearized sensitivity formulation to model cost function and constraint information for an NPSOL solution to the optimization problem. As a result of the use of transpiration boundary conditions a relofting process is required to further improve the optimization when the TRANAIR solution adaption has reached the last grid refinement. Once relofted the geometry can be further optimized, as the geometry perturbations are better represented. For the TRANAIR optimizations presented herein only one such relofting process was performed. The geometry perturbation routine or design variable library from 3DOPT was interfaced with TRANAIR to provide a consistent set of geometric perturbations among the three approaches.
Finally the 3DOPT system was modified to provide
gradient driven searches using NPSOL with direct coupling to the flow analysis
routines. For the purposes of the present study, one-sided finite differences
were used to provide derivatives for the non-linear constraints and objectives
to the optimizer. For better efficiency, the inputs were configured such
that NPSOL used a linearized model during the line search portions of the
optimization. The design variables were also normalized to a constant range
to enhance NPSOL’s convergence. This version of the system is designated
3DOPT-D.
Summary of Test Case
The test case was first reported by Lovell and Doherty
(Ref. 11) as a demonstration of their design technique,
a local, gradient based approach. It was later included in the 3DOPT development
contract as a system demonstration case. The geometry consists of an area-ruled
body and an untwisted wing with 45o leading edge sweep and unswept
trailing edged as described in reference . The wing section is a NACA64a005
section, constant along the span. The design problem was formulated as
a multi-point drag minimization with two design conditions specified as
described in Figure 2. Weighting factors of 0.75 and 0.25 were applied
to the transonic and supersonic drag data, respectively, with the weighted
sum defining the cost or objective function for the optimization. Design
variables specified were intended to represent those used in the previous
Lovell study. A total of 22 design variables, comprised of twist, camber
and vehicle angle-of-attack, were used. Four twist and four camber mode
variables with each camber mode using four chordwise distributed design
variables were defined at span locations 286., 457., 628., and 800., along
with an angle-of-attack variable at each design point.
Flow Analyses
Flow analyses for the optimizations were all completed
using inviscid physics. Within the 3DOPT system TLNS3D was used in Euler
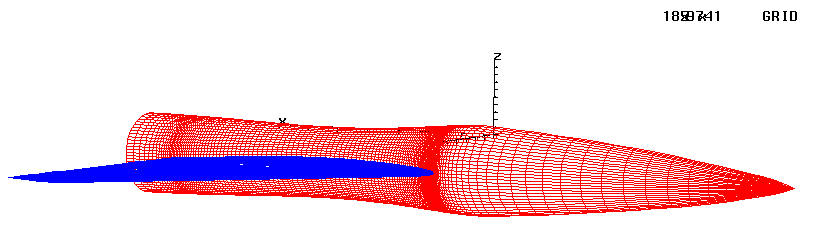
mode with a 185 by 97 by 41 OH grid. The surface grid, which formed the
basis of the inner boundary for a single zone HYPGEN generated volume grid,
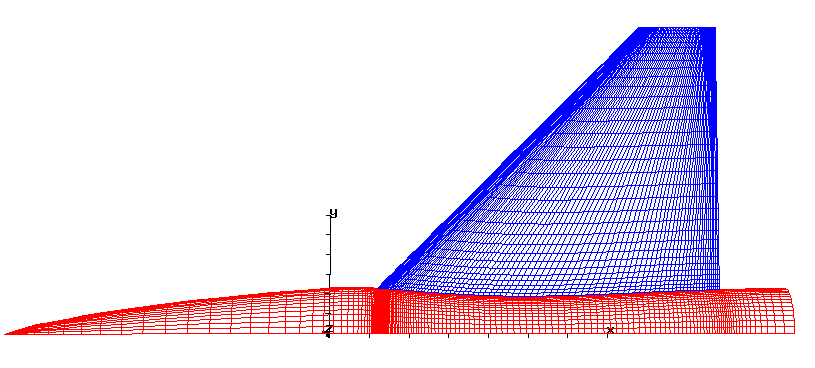
is illustrated in Figure 3. The field grid in the plane of symmetry is
shown in Figure 4. This topology produces a grid density with 101 points
each over the upper and lower wing surfaces. The TRANAIR flow solutions
were produced using the solution adaptive grid options available with a
total of approximately 400,000 boxes or cells as seen in Figure 5. The
same surface grid as pictured in Figure 3 was used to represent the geometry
within TRANAIR. Given the restricted volume domain boundaries used with
TRANAIR, this grid density is considered a fine or highly resolved grid.
 |
 |
 |
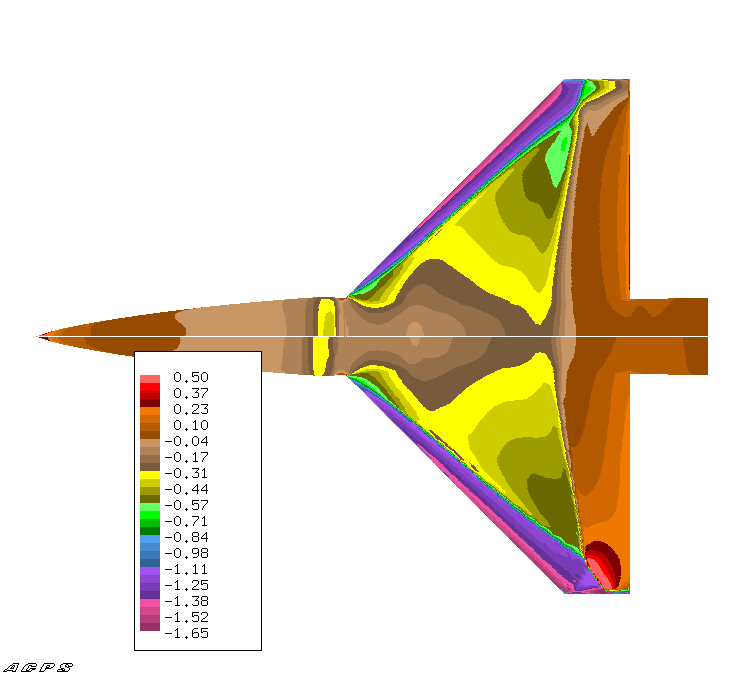
A comparison of the seed geometry analysis results for both TLNS (top) and TRANAIR (bottom) can be seen in Figure 6. Both solvers give similar results with the TRANAIR solution having a better resolution of the shock due to its adaptive gridding capability.
Description of Refinement Strategies
Using the 3DOPT system several schemes for conducting a global design space search were examined. These schemes are basically different means of adding points to an initial population of sites or design vectors used to model the design space. Approximate models within 3DOPT are known as kriging models that interpolate the responses in a manner that minimizes the error at untried locations within the population data set as described in reference . Three different initial population sizes were examined, 54, 125 and 243. In addition to population refinement of the models from these initial data bases, the local gradient driven approaches were also used as a refinement step in the design space search. These approaches are summarized below.
Approach 1 - Simple iteration - Create a model from an n sample size, find the optima from the model, run confirmation flow solutions at the optima, add these runs into the design space data base and repeat
Approach 2 - Model refinement using an engineer in the loop, basing refinement decisions on available model characteristics, i.e., design variable main effects and interactions, to restrict the range of design variables to areas of design improvement as identified by the current model
Approach 3 – Stratified balanced local-global search (SBLGS) model refinement method, where points are systematically added locally near a model optimum and globally at points throughout the design space where model errors are large.
Approach 4 - Refine approximate global model
predicted design with local gradient driven approach with starting points
defined by observed optima from the approximate model
Results
Baseline Approximate Model
An initial design space search was completed as described
in reference using the 3DOPT system. This was based on a 125 site approximate
model requiring 250 distinct Euler solutions. The results of this design
space search are summarized in Table 1. During optimization, two candidate
optima were identified from the model. These are indicated in Table 1 as
Opt 1 and Opt 2. Also included in the table are the baseline aerodynamic
characteristics. The values listed in Table 1 are all based on post-optimization
confirmation runs with TLNS3D. Some significant reductions in the objective
function were obtained at both of the optima observed – 18.5 and 16 % for
Opt 1 and Opt 2, respectively. These were obtained through improvement
of the transonic design point at the expense of the supersonic design point
consistent with the weightings applied to each design point. The trades
that can be obtained via different weighting functions between the two
design points are well documented in reference and have been extended in
reference .
|
|
|
|
|
|
|
| Seed Configuration: Objective Function Value = 0.03214 | |||||
| M = 0.9 |
|
|
|
|
|
| M = 1.6 |
|
|
|
|
|
| Opt 1: Lowest Model Objective Function, Confirmed Value = 0.02619 (-18.51%) | |||||
| M = 0.9 |
|
|
|
|
|
| M = 1.6 |
|
|
|
|
|
| Opt 2: Second Local Optimum, Confirmed Value = 0.02698 (-16.05%) | |||||
| M = 0.9 |
|
|
|
|
|
| M = 1.6 |
|
|
|
|
|
Direct Driven Benchmarks
Our focus here is on relative performance of the
IRS approximate modeling approach and potential refinement schemes for
a global design space search. To benchmark this performance we used the
results from the direct driven optimization methods. In Table 2 results
from TRANAIR and 3DOPT-D are compared, all starting from the same seed
geometry. For the TRANAIR and the 3DOPT-D designs, the side of body wing
section is frozen as it was for the approximate modeling applications.
Note all numbers presented for TRANAIR are based on TLNS3D confirmation
runs.
|
|
|
|
|
|
|
|
| Seed Configuration Objective Function Value = 0.03214 | ||||||
| M = 0.9 |
|
|
|
|
|
|
| M = 1.6 |
|
|
|
|
|
|
| Multi-point Opt TRANAIR, Objective Function Value = 0.02594 (-19.29%) | ||||||
| M = 0.9 |
|
|
|
|
|
|
| M = 1.6 |
|
|
|
|
|
|
| Multi-point Opt 3DOPT-D, Objective Function Value = 0.02456 (-23.58%) | ||||||
| M = 0.9 |
|
|
|
|
||
| M = 1.6 |
|
|
|
|
|
|
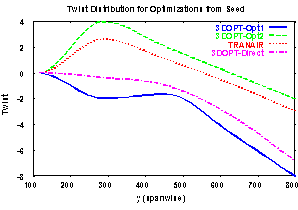
Based on an angle of attack comparison it appears
that the two gradient driven approaches are moving to different points
in the design space, the TRANAIR result corresponding to the second optimum
observed with the 3DOPT approach and the 3DOPT-D result corresponding to
the first optimum. This is further supported by the twist distributions
described in Figure 7. The TRANAIR results are clearly aligned with the
second optimum from the 3DOPT results, Opt 2, and the 3DOPT-D results are
aligned with the twist distribution corresponding to the 3DOPT Opt 1 result.
Although no convergence study of difference increments was completed for
the 3DOPT-D results, it is likely that the differences between TRANAIR
and 3DOPT-D results are a consequence of relatively large finite differences
used in 3DOPT-D.
From a computer resource standpoint, the 3DOPT process required 125 flow solutions for each design point or 250 total flow solutions. The TRANAIR process required the equivalent CPU time of about 60 TLNS3D flow solutions. The 3DOPT-D design required 7 major design iterations to reach the specified drop tolerance. This corresponds to 369 TLNS3D flow solutions. For comparison, only three major iterations, or 138 TLNS3D flow solutions, were required by the 3DOPT-D approach to achieve the objective level of .0259 produced by the TRANAIR approach.
Comparisons were made between the current work and those from reference 11. The results from 3DOPT-D were found to be equivalent to those reported in reference 11 when differences in configuration modeling and design problem formulation were taken into account. A detailed description of these comparisons is beyond the scope of this paper.
Comparison of Refinement Strategies
Results from various refinement strategies examined
are presented in Figure 8 through Figure 10 and Table 3 through Table 6.
In the figures we introduce model errors as additional metrics of performance
where model error was determined as the percentage difference between model
prediction and subsequent confirmation analysis at the model predicted
design vector settings. For the current 3DOPT applications three models
were used, an objective function model and two lift constraint models.
The figures present an iteration history of model error while the tables
compare the baseline 125 site model results with final iteration objective
function values for a given refinement strategy. Objective function values
listed in the tables are from post-optimization analysis where the angle-of-attack,
?, at each design condition was adjusted to meet specified lift constraints.
The model predicted and required angles-of-attack are also presented in
the tables as another measure of modeling error.
|
|
|
|
|
|
|
|
| Baseline 125 Site Model | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 125 Site Model: Refinement Iteration 3 (130 Sites Total) | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 54 Site Model | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 54 Site Model: Refinement Iteration 6 (65 Sites Total) | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| Opt 3 |
|
|
|
|
|
|
| 243 Site Model | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 243 Site Model: Refinement Iteration 3 | ||||||
| Opt 1 |
|
|
|
|
|
|
Approach 1
Listed in Figure 8 and Table 3 are the results from Approach 1 refinement scheme as applied to 54, 125 and 243 site 3DOPT approximate models. For the 125 and 243 site starting points this simple iteration scheme consistently reduces the objective function model error with each iteration cycle, as displayed in Figure 8. The 54 site data, however, demonstrates no consistent trend. The objective function error displays a sharp increase on the sixth iteration with the 54 site data set, an event that is also shared by the lift constraint model errors from the 243 site data set. The relatively small constraint errors result in only slight changes to the angle-of-attack required to adjust lift levels to target values during confirmation runs, as indicated in Table 3. However, this iteration scheme does not produce any consistent improvement in constraint model errors. Resulting objective functions do benefit from the application of this iteration approach for the 54 and 243 site data sets but not with the 125 site case. Also observed with all three cases was a change in the character of the design space model where the number of local optima observed varied over the iteration history.
The picture is also complicated by the presence of
multiple optima. The data presented in Figure 8 and Table 3 are tracking
local predicted optima by their relative objective function value, i.e.,
opt 1 represents the lowest objective function value from the models for
any given iteration and opt 2 the next highest value and so
on. This is done without correlating the actual location in the design
space with an objective function value. It has been observed during some
of the iteration cycles that the location in the design space associated
with a predicted minimum objective function flip flops back and forth between
the various locations.
Approach 2
Two variations of Approach 2 were examined. In the first, the geometry associated with opt 1 of the basic 125 site data set was used as a seed or starting point for a second 3DOPT system application. This second application was accomplished using a new, 50 site experiment with the same set of design variables as the initial optimization. However, a restricted range of variation was imposed on a selected number of these design variables. Six of the 22 design variables were selected on the basis of the magnitude of objective function sensitivities. These were the two angle-of-attack variables and the four twist variables. The second variation of refinement Approach 2 consisted of adding 50 new sites to the basic 125 site data set. The new sites were selected in two bands, or strata, of angle-of-attack that bracketed the settings for opt 1 and opt 2 from the baseline 125 site model. Angle-of-attack was selected, again on the basis of main effects, because these design variables had the greatest influence on the objective function. These new sites were combined with the original 125 sites to create models based on 175 data sites.
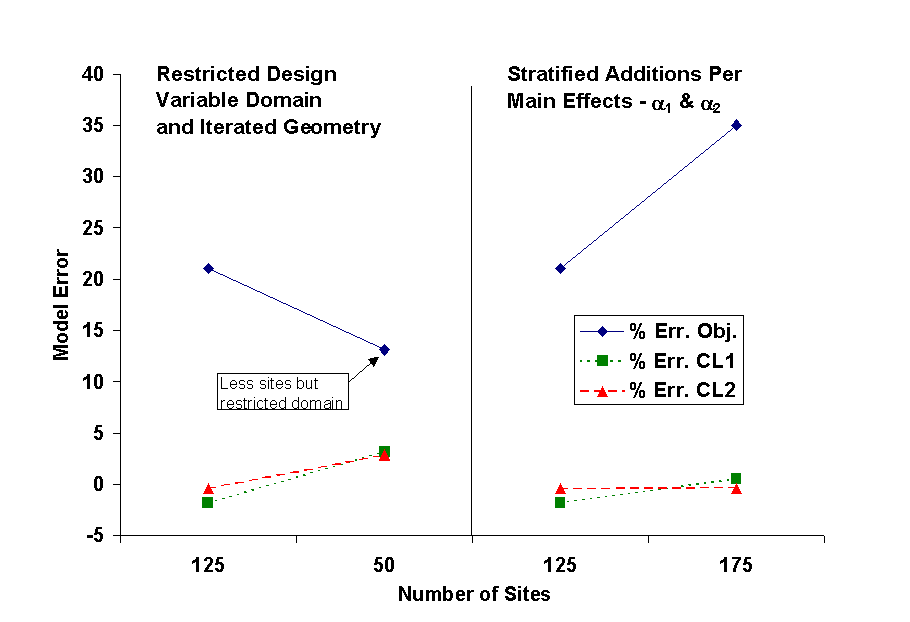
Results for refinement Approach 2 are presented in
Figure 9 and Table 4. From a model error perspective described in Figure
9, the first variation produced a reduction in objective function model
errors with a slight increase in constraint model errors. There was also
a further decrease in the objective function as indicated by the opt 1
result in Table 4 that was larger than any of the refinement Approach 1
results including the 243 site data. The second variation of this approach
was not successful. A significant increase in objective function error
was accompanied by only a slight decrease in constraint model errors. Associated
objective function values increased over those observed with the basic
125 site model.
|
|
|
|
|
|
|
|
| Baseline 125 Site Model | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 50 Site Model: Restricted design variables, iterated geometry | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| Opt 3 |
|
|
|
|
|
|
| 175 Site Model: Stratified additions about ?1 and ?2 | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
Approach 3
Investigation of Approach 3 focused on the 54 site
data set with the general target of refining to the 125 site population
level. Three variations of the SBLGS refinement strategy were pursued.
In the first, a single refinement iteration was completed with the addition
of 71 new points all selected using the local, low objective value, constraint
matching point selection method. The results for this approach are designated
Option A in Table 5. The second variant examined was comprised of three
refinement iterations, each of which targeted 16 new points using the local
component of the SBLGS method and 9 using the global component, in sequential
iterations. Results from the final 123 site model are designated Option
B in Table 5. The third variant consisted of two SBLGS iterations but with
an interim model construction between each iteration that used the confirmation
results at predicted optima from the previous model, i.e., a hybridization
of Approach 1 and 3. The results from the second iteration, 107 site model
are designated Option C in Table 5. In Figure 10 the iteration histories
for these three options are shown.
From Figure 10, it can be seen that all of the three variants of Approach 3 generated objective function model error reductions greater than that associated with the baseline 125 site model. Note that Option C of Approach 3 achieved the greatest level of reduction of the three with only 107 total data sites maintaining a steady reduction in error with each iteration. Among the three options constraint model errors were marginally better with Option A while Option C produced an increase in lift constraint 2 (supersonic point) model error. With the exception of Option C, lift constraint 2, all three variants resulted in lower constraint model errors than the baseline 125 site model.
Each of the three options did produce improvement in their respective
objective function values through the iteration process. However, the data
from Table 5 indicate that the results of all three variants of Approach
3 failed to improve over the minimum objective function observed with the
baseline 125 site model. Comparison of the angles-of-attack in Table 5
for each of the three variants of Approach 3 with the baseline 125 site
values suggests a more favorable evaluation. A single optimum is generated
by each of the three variants but in different areas of the design space.
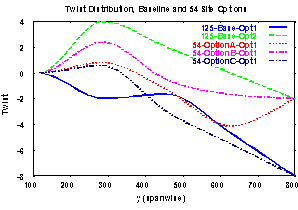
Further support of this is provided by the twist comparisons in Figure
11, where Options A and C are aligned with Opt 1 from the baseline 125
site model and Option B with Opt 2 from the baseline model. If a comparison
is made with the baseline model Opt 2 results, then Option B variant of
Approach 3 generates an improvement over the baseline of 1% or 3 drag counts
(0.0003). On the basis of trends observed with Option C, it is also expected
that Option C results, at an equivalent number of data sites, would out
perform the baseline 125 site model.
|
|
|
|
|
|
|
|
| Baseline 125 Site Model | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| Option A: Iteration 1, 125 total sites | ||||||
| Opt 1 |
|
|
|
|
|
|
| Option B: iteration 3, 123 total sites | ||||||
| Opt 1 |
|
|
|
|
|
|
| Option C: iteration 2, 107 total sites | ||||||
| Opt 1 |
|
|
|
|
|
|
Approach 4
The final refinement method examined used the optimal geometry resulting from the first, or lowest, of the two observed optima from the baseline 125 site data set as a starting point for direct driven optimizations. Separate optimizations from the second optimum were also completed using the TRANAIR design system. Table 6 summarizes the result of this refinement approach. Both the TRANAIR and 3DOPT-D approaches produced improvements over the objective functions obtained when starting from the initial geometry. The 3DOPT-D approach produced only a slight improvement of three drag counts. The TRANAIR approach benefits significantly from the iteration placing it nearly at the performance level of the 3DOPT-D.
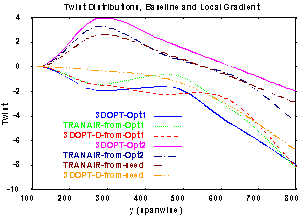
These results also support the bi-nodal characteristics
of the design space. On the basis of angles-of-attack from Table 6 and
twist distributions shown in Figure 12, the two optima observed with the
baseline 125 site model are clearly tracked by the TRANAIR results. These
two areas in the design space, however, produce essentially an equivalent
reduction in objective function given the specified multi-point weighting
factor. As the results of reference indicate, this is consistent with a
pareto analysis of the data across the complete multi-point design space.
The 3DOPT-D approach required 9 major iterations
to reach its objective function value, which corresponds to 414 TLNS3D
flow solutions for both design points. TRANAIR, however, required an equivalent
CPU time of about 60 TLNS3D flow solutions.
|
|
|
|
|
|
|
|
| 125 Site Model: Iteration 1 | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| TRANAIR from 125 site Optimum Geometries | ||||||
| Opt 1 |
|
|
|
|
|
|
| Opt 2 |
|
|
|
|
|
|
| 3DOPT-D from 125 site Optimum Geometries | ||||||
| Opt 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusions
Irrespective of refinement approach there were two trends consistently observed throughout the study. First, the models were always optimistic predictors of objective function values, i.e., they under predict confirmed objective function values. Second, with few exceptions, model errors associated with objective function models were higher than corresponding lift constraint model errors by one to two orders of magnitude. The former is most likely a consequence of the characteristics of the surface fit where, depending on computed interpolation parameters, there is an oscillation of function values between neighboring data points. The latter remains an open question.
The approximate models examined are useful tools for the global exploration of a design space. They do not yet compete with direct driven methods for identifying local optima for a given objective function formulation. On the other hand, they do allow one to quickly look at optima corresponding to various objective function formulations, such as different design point weightings, without having to recalculate the flow solutions
For the 22 variable design case examined 125 sites provided a general picture of the design space. The 54 site case was inadequate. The 243 site model provided no significant improvement in design space modeling.
Overall, refinement strategies based on model only approaches provided only marginal improvement of objective function value compared to direct driven approaches. The engineer in the loop (Approach 2) refinement strategy provided the best improvement in objective function of Approach 1 through 3. SBLGS was a close second and is much more amenable to an automated procedure. SBLGS needs modification to allow point additions for multiple model optima.
Refinement strategies using an approximate model global design space search combined with local, direct driven refinements were shown to produce results superior to direct driven alone.
The computational costs cited for the 3DOPT-D, finite
difference, derivative calculation methods were included as a rough guideline.
These costs can and should be adjusted for alternative derivative calculation
methods. Resource requirements quoted will be significantly lowered for
direct driven methods using adjoint or sensitivity formulations to calculate
derivative information. These may also play a role with approximate modeling
approaches.
Acknowledgements
Portions of this work were completed using 3DOPT,
developed for the Air Force Research Laboratory (formerly Wright Laboratory),
Wright-Patterson AFB, Ohio, under the 3-Dimensional Design Optimization
contract, number F33616-94-C-3001. Acknowledgment is also given to NASA
for the technology contributions to several of the system modules. Finally,
thanks are extended to our review committee, Matthew J. Warfield, David
A. Treiber, Evin J. Cramer and Andrew J. Booker, for many helpful suggestions.
References
2 Herling, W. W., Blom, G. A, Booker, A. J., LeDoux, S. T., Ratcliff, R. R., Treiber, D. A., Warfield, M. J., "3-Dimensional Design Optimization, Final Report", WL-TR-97-3054, DTIC AD B231624, April 1997.
3 Herling, W.W., Emsley, H.T., LeDoux, S.T., Ratcliff, R.R., Treiber, D.A., Warfield, M.J., "3DOPT - An Integrated System for Aerodynamic Design Optimization", AIAA Paper 98-2514, June 1998, 16th Applied Aerodynamics Conference, Albuquerque, NM.
4 Young, D. P., Huffman, W. P., Melvin, R.G., Bieterman, M. B., Hilmes, C. L., Johnson, F. T., "Inexactness and Global Convergence In Design Optimization", AIAA 94-4386, September 1994.
5 Boeing Information & Support Services, "DT_NURBS Spline Geometry Subprogram Library Reference Manual Version 3.1," Naval Surface Warfare Center/Carderock Division, David Taylor Model Basin, November 1995.
6 Booker, A. J., Case Studies in design and Analysis of Computer Experiments, ASA Proceedings of the Section on Physical and Engineering Sciences, 1996, pages 244-248, Alexandria VA, 1996.
7 Chan, W.M., Chiu, I.T., and Buning, P.G., "User’s Manual for the HYPGEN Hyperbolic Grid Generator and the HGUI Graphical User Interface," NASA TM-108791, October 1993.
8 Vatsa, V. N., "Accurate Numerical Solutions for Transonic Viscous Flow Over Finite Wings," Journal of Aircraft, Vol. 24, June 1987, pp. 377-385.
9 Holst, T. L., "Fast, Conservative Algorithm for Solving the Transonic Full-Potential Equation", AIAA Paper 79-1456, July 1990.
10 Gill, P. E., Murray, W., Saunders, M. A., and Wrigth, M. A., "User’s Guide for NPSOL (Version 4.0): A FORTRAN Package Nonlinear Programming", Stanford University Technical Report SOL86-2, Department of Operations Research, 1986.
11Lovell, D.A., Doherty, J.J., "Aerodynamic Design of Aerofoils and Wings Using a Constrained Optimisation Method", ICAS, 1994, Anaheim, CA.
12 Sacks, J., Welch, W. J., Mitchell, T. J. and Wynn, H. P., Design and Analysis of Computer Experiments, Statistical Science, 1989, Vol 4, No. 4, pages 409-435.
13 Booker, J. A., "Design and Analysis of Computer Experiments", AIAA 98-4757, September 1998, St. Louis, MO.
14 Cramer, E.J., "Using Approximate Models for Engineering Design", AIAA Paper 98-4716, September 1998, St. Louis, MO.
* Senior Principal Engineer, Senior Member AIAA
† Senior Specialist Engineer, Member AIAA
Copyright © William W. Herling. Published by the American
Institute of Aeronautics and Astronautics Inc., with permission.