
This paper presents the results of a three-year contract to develop a 3-Dimensional Design Optimization (3DOPT) system for the Air Force Research Laboratory (formerly Wright Laboratory) under Contract F33615-94-3001. Development work under this contract has led to the release of an optimization system that will perform wing alone, or wing in the presence of a body, optimizations using potential flow, Euler or Navier-Stokes level physics in an automated, approximate model framework. Target turnaround times of 3 days for Navier-Stokes and 1 day for Euler flow analyses are achievable with this. The released 3DOPT system is comprised of a collection of technology modules that address all aspects of the optimization process.
In the early 1990’s much of the activity in wing optimization was focused on inverse design methods. Although design improvements were often realized with these design-to-pressure methods, their need for a priori knowledge of the final design characteristics and their failure to guarantee an optimal design limited their applicability. During this same time period efforts to reduce the costs of producing new aircraft focused on attempts to reduce the design cycle time, and the number of design iterations. By introducing advanced analysis techniques early in the design process it was believed that only the best designs would reach the test and evaluation stages. To maximize the effectiveness of the design process a multi-disciplinary approach that balances the needs of many disciplines (aerodynamics, structures, flight controls, etc.) was needed but in practicality was beyond the reach of the technology at the time. It was determined, however, that a good first step towards that final goal would be a capability that could optimize an early design within a single discipline. Thus was born the idea of what has become the 3DOPT system. In 1994, the Air Force issued a challenge to develop an aerodynamic design optimization capability. The Boeing Company won the contract and began development by leveraging off loosely coupled tools developed internally.
In general, the implementation of design optimization algorithms can be divided into two categories, direct driven or approximate modeling. In the former, all information required by the optimization search is provided by direct interaction with the CFD flow solver. With the latter, however, the design space is sampled at a select number of points, or sites. This subset of information is then used to construct a model of the response of the product, usually drag or some other aerodynamic characteristic, as a function of changes in design variables, usually geometric characteristics. The optimization search is then performed using the response model to supply necessary information.
3DOPT is a design system that uses approximate modeling of the design space. It is capable of identifying geometry perturbations to a wing design that will improve, if possible, the aerodynamic performance of the wing according to some specified criteria or objective function. It is an engineering tool that assists the designer in the search for an improved product using the technology of numerical optimization. The system provides a means to explore a design space, from a global perspective, that may be characterized by multiple local optima. As a consequence of this exploration, information about the relative influence of the design variables on wing performance is obtained as well as areas within the design space where the performance is improved.
Development of the 3DOPT design system was driven by several operational objectives and constraints. On a top level the goal was to provide an aerodynamic design capability for wing alone or wing in the presence of body geometries. Target design turn around times were set at one day for Euler level physics and three days for Navier-Stokes level physics. These were supplemented by several sub-goals: accuracy, flexibility, ease of use and computational efficiency.
Accuracy was considered from two perspectives, level and range. The philosophy was to provide as accurate a process as possible but also provide a range of physics to allow a trade between accuracy and cost. The goal for flexibility was to provide a framework that would permit convenient inclusion of emerging technologies or extensions to the scope of the system.
Guidelines adopted during system development to promote ease of use included minimizing the inputs required of the user, and providing elements of automation wherever possible. Also contributing to productive application of design tools is the computational efficiency of the system. Computational efficiency influenced selection criteria for all elements of technology within the 3DOPT system.
At all points in the 3DOPT process the relative computational cost is under the control of the user. Computational resources and analysis times required for an optimization study vary directly with the fidelity obtained with the approximate modeling approach of 3DOPT. The system has been designed to maximize the information obtained about a design space for a given investment of resources while allowing for a metering of resources expended during the design process.
In addition to performance objectives and operational attributes, the design of the 3DOPT system was also influenced by system design constraints. In order to establish software release flexibility, the inclusion of third party, licensed or proprietary, software was not considered. The use of existing, non-proprietary software, without modification, was emphasized to reduce system development cost. Also, acknowledging the importance of geometry in the design process and the expense of its development, a compromise between generality and usability was maintained.
The initial implementation (version 1.0) of 3DOPT operates with wing alone or wing/body configurations. However, with wing/body configurations, only the wing geometry can be changed by the system with the wing root geometry remaining fixed. A new version of the system, currently under development, will allow changing of the wing root geometry and include a body design capability.
Specific capabilities of the system include:
The following sections will give an overview of the 3DOPT system and it's major components, followed by a discussion of a sample optimization test case using the system. For a more detail description of 3DOPT please refer to the 3DOPT User's Guide (Ref 1) and Final Report (Ref 2).
An overview of the 3DOPT system is illustrated in Figure 1. The main components of the system, and the process steps in a design application with 3DOPT are shown. The major software components of the system are the David Taylor NonUniform Rational B-Spline (DTNURBS, Ref 3) geometry library, Design and Analysis of Computer Experiments technology library (DACEPAC, Ref 4), HYPGEN (Ref 5), TLNS3D (Ref 6), TWING (Ref 7, Ref 8), NPSOL (Ref 9), and BGENETIC. DTNURBS provides geometric functionality within 3DOPT supporting the geometry input, surface gridding and geometry modification modules. DTNURBS is a library of primitive geometry operations that can be included in FORTRAN routines to perform higher order geometry tasks. Development of the DTNURBS technology is being pursued by Boeing Shared Services Group (SSG) under contract to the US Navy. Elements of the DACE library have been implemented in the design experiment, approximate modeling and optimization modules of 3DOPT. The DACE technology library is comprised of the three main elements, experiment generation, response surface model fit and model interrogation-evaluation. This also is a Boeing developed product within BSS. HYPGEN, a hyperbolic grid generation program developed by NASA, provides volume grid generation functionality within 3DOPT. TLNS3D and TWING, also NASA products where the former is an Euler/Navier-Stokes CFD flow solver and the latter a full potential flow solver, constitute CFD capability within the system. NPSOL, a gradient optimization program developed by Stanford University, and BGENETIC, a Boeing developed hybrid genetic-gradient optimization routine, provide technology support within the optimization module. The control of the system process and communication between modules are maintained by a collection of control scripts and a Graphical User Interface (GUI).
The following sections will discuss the major components
of the 3DOPT System.

Geometry and Surface Gridding
As two stipulations of the 3DOPT development contract were to avoid using commercially licensed software, and to develop the system in FORTRAN, the DTNURBS library was selected as the geometric data structure of the system. The DTNURBS routines also provided an easy way to include higher order geometric manipulation with full NURBS support, which is becoming a computer aided geometry design standard. DTNURBS also fully supports NASA-IGES and is under continued development through funding from the Navy, NASA Lewis and others. It is available to all government contractors with a license acquired from the U.S. Navy.
The aforementioned DTNURBS features will allow for greater flexibility in future expansion of the 3DOPT system for handling more complex geometries, such as wings and bodies defined with multiple trimmed IGES surfaces. In addition this flexibility will allow for integration of unstructured flow solvers. Enhancements to the 3DOPT system for handling wing root and body geometric perturbations are in progress.
Using the DTNURBS library, four specific 3DOPT-geometry functions were created: geometry input, surface geometry gridding, geometry perturbation, and geometry constraint evaluation.
Geometry Input
Geometric input was accommodated by developing three different forms. For existing wing lofts an input option was created for reading IGES files, where the wing or body loft is represented by a single B-spline surface (IGES Type 128). It was not intended to develop a full-blown CAD system, hence the single surface limitation for IGES loft inputs. In support of existing grids, options have been provided for grid input via simple ASCII and PLOT3D file formats. Lastly for cases where the user does not have explicit geometry, seed surfaces can be created using parametric loft options for the wing and body. In addition to the above input options the user also has the ability to modify the seed surface geometry by selecting a seed airfoil for replacement in the wing surface, e.g., one could replace all airfoils in an IGES B-spline wing with NACA 0012 airfoils.
Surface Gridding
Surface gridding in the 3DOPT system is performed on the seed input NURBS surface, whether the seed was a surface fit through input grids, an IGES surface input, or a parametric loft. Surface gridding options, with user input spacing, were developed for clustering grid points about leading and trailing edges, wing spanwise break points, and body nose, tail, crown and keel locations. The default distribution function used in the gridding process is the hyperbolic tangent function. Grid points are computed in either arc length or parametric space of the surfaces, with parametric gridding being faster. For wing body cases the input wing and body seed surfaces are intersected and these trimmed surfaces are then used to create the final seed surface grids for use in the proceeding steps. In instances where existing surface grids have been read into the system, the grids can be used as-is and the surface gridding step can be skipped.
Geometry Modification
Creation of the geometry perturbation or design parameter library was based on the idea of perturbing the seed wing grid file, where the grid lines resemble buttock line (wing section) cuts. Here the perturbations are applied to the seed wing grid file with both the wing root section and body grid fixed for wing-body cases.
As with other geometry aspects of the system the geometric perturbation options rely on DTNURBS, where B-spline curves for each of the wing airfoil sections are fit. Although this is better than using grid points it is not as good as using NURBS surfaces. The idea of using NURBS surfaces for this step was dropped in favor of fitting curves to each local wing section to increase speed, robustness, and perturbation flexibility.
One reason behind using curve fits of the seed grid over the seed surface loft was that the original surface knot distributions may not be fine enough to properly capture spanwise or chordwise perturbations. For example, when trying to perturb a surface consisting of two spanwise knots with a cubic variation, only linear variations could be captured in the spanwise direction as only two knots exist. One possible solution could have been to perform surface patch degree raising and knot insertion but this can be a tricky task and can result in severe continuity problems at patch boundaries. With the surface grid approach, a grid with 20 or so sections in the spanwise direction would amply capture any cubic variation that the optimizer might request. In addition to the above issues, using surface grids with grid lines arranged in airfoil sections allowed for a more explicit definition of design variable options, such as airfoil camber or thickness.
The geometric perturbation options for the wing are broken up into wing local perturbation and wing gross perturbation options, as listed in Figure 2 (with examples). Local wing perturbation options are selected and applied in the spanwise direction. During an optimization the current value of each design variable will be spline fit as a function of span, where the curve fits are either piecewise monotonic cubics, or higher order user selectable polynomials. The curves are then used to apply perturbations at each airfoil section across the span. The design variable options (Figure 2) are, for the most part, self-explanatory with the exception of the camber or thickness options. Two methods are used for camber and thickness perturbations. One method involves the application of four Hicks type functions (modes). The other option is to use DTNURBS splines, with user specified chordwise knots, where the optimizer explicitly perturbs the knots. Wing gross design library options listed in Figure 2 apply to the entire planform of the wing, and will result in planform changes.
Geometry Constraints
The wing sectional constraints are local to each airfoil,
and are computed along each constant-span grid line. These include the
options from twist to local thickness as listed in Figure
2.
Spanwise variation of local constraint variables was
allowed for by using the same method applied in the geometry modification
library. Here the user specifies constraints at discrete span locations
and then spanwise monotonic curve fits are created. Evaluations of this
constraint curve fit are used for points between the user input defining
locations. Sectional properties for each individual wing are computed across
the span and then output in a file. A sample of the types of sectional
properties computed is shown in the upper right of Figure
2. Gross constraints refer to constraints that exhibit two-dimensional
variation across the planform, such as wing area and curvature. For the
curvature constraints two methods are available for computing the curvatures,
a finite difference approach applied to the grid points or a DTNURBS surface
fit and evaluation. In either case the curvatures in the span and chord
are computed for the entire grid and output to a curvature data file, along
with the pass or fail. In addition to applying the curvature constraints
across the entire span of the wing an option has been provided to also
allow specific areas of the wing to be constrained. These areas or bounding
boxes are specified as pairs of normalized chord and span locations to
define polygons that trace out the desired constraint region.
Field Gridding
The key to successful automated grid generation is reliability and robustness. The methods must be sufficiently automated so that the interactive user inputs are minimal or generated internally, and the methods must be able to handle the required classes of geometries as the optimization proceeds. Good grid quality may require some initial user tuning of the chosen method, but subsequent grids of modified geometries must be automatic. At the beginning of the development effort in 1994, several mesh generation methods were evaluated on this basis, and a single approach was chosen.
The three approaches considered were hyperbolic, algebraic, and elliptic. The hyperbolic method examined was the NASA-Ames HYPGEN code, and the algebraic and elliptic methods were from GRIDGEN3D, an Air Force and NASA-Ames product. These particular codes were chosen because they were readily available, familiar to the code developers, and existing as non-proprietary software.
3D elliptic grid generation methods are capable of producing high quality grids for many applications. They are, however, comparatively slow, and require more setup time and effort because all domain boundaries must be specified a priori. 3D algebraic methods are extremely fast, but they also require that all domain boundaries be generated beforehand. Furthermore, interior grid point distribution is mostly dependent on boundary distributions, so unless the boundary grids are carefully controlled, grid quality is diminished.
Hyperbolic grid generation methods hold advantages that made them the best selection for 3DOPT. They are relatively fast, require minimal setup information, yet they can produce high quality grids for viscous flow analysis. As long as the classes of problems to be examined are limited, the only inputs required are the surface grid and a few numerical tuning parameters. The other grid domain boundaries are generated right along with the interior points. The weakness of this approach is that the robustness of the hyperbolic grid generator is dependent on the distribution of surface grid points and the shape of the domain. The user must often tune the case by trial and error to find the numerical settings necessary for a successful grid. Extensive testing has shown, however, that for the class of problems encompassed by 3DOPT, once the first grid has been generated successfully, subsequently modified surface grids can proceed automatically with no further user input changes.
As part of 3DOPT development, the numerical smoothing scheme in HYPGEN was enhanced to increase robustness. One peculiarity of the 3DOPT environment is that sparse, single-block grids are used to decrease CFD analysis time. HYPGEN reliability breaks down when large normal distance steps are taken, as is the case when an extensive, sparse grid is desired. Additional tuning parameters were added to the code to make an extended sparse grid easier to generate. Lack of surface grid smoothness and the presence of surface shape discontinuities, such as at a sharp wing leading-edge can also decrease HYPGEN reliability. These effects also appeared in many 3DOPT test cases. Sharp surface shape discontinuities introduced grid problems that were not solvable by any means within HYPGEN. A simple post-processing utility was written to handle these areas, within a batch script so as to preserve automation. The utility uses a DTNURBS based splining method to redistribute points near the surface at a sharp corner where the mesh may have negative volume cells due to over smoothing.
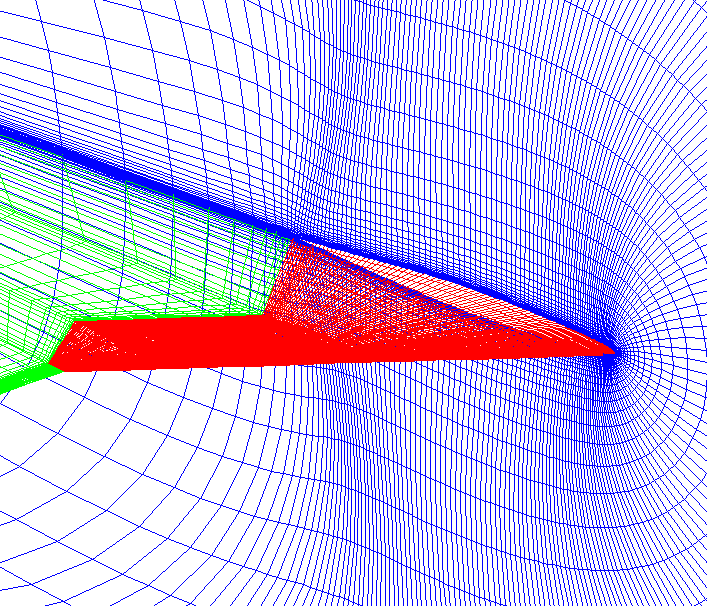
In developing the field gridding strategy, reliability, quality, and automation were all factors, but automation was considered paramount. Therefore, the same grid arrangement and domain topology are used in all 3DOPT cases. For the cases of wing-only or blended wing-body optimization, a c-h grid is always used, where the c-direction is longitudinal along airfoil sections, and the h-direction is spanwise. (Figure 3)
A c-h grid contains fewer grid degeneracies, e.g., an axis, than an o-h grid (o spanwise), and also produces generally good orthogonality and smoothness. For discrete wing-body cases, where the c-grid on the body near the wing-body juncture would be highly skewed, an o-h topology was instead used, where the o-direction is spanwise. (Figure 3)
Not only does this arrangement decrease grid skewness, it also follows the natural geometric basis of the body (crossections stacked streamwise). This will simplify much of the work of implementing the body design feature into future versions of 3DOPT.
Finally, a pre-processing utility was written to concatenate
the grids output from the surface gridding module and algebraically generate
the necessary wake grid points to complete the surface grid necessary for
HYPGEN processing. The wing alone grid pre-processor closes the wingtip
section to a slit, and generates the wake planes downstream of the trailing
edge and outboard of the wingtip using 3D transfinite interpolation. The
wing-body pre-processor closes the wingtip and generates wake planes upstream
of the wing leading edge and downstream of the wing trailing edge.
 |
 |
Flow Solver
Central to the requirements of the 3DOPT design system is an Euler/Navier-Stokes level analysis capability. From the large number of codes within this class that are generally available, two were selected for participation in a trade study with the goal of selecting one for integration into the optimization package. These codes were the CFL3D (Ref 10) and TLNS3D (Ref 6) codes from NASA-Langley. These two codes represented the best opportunity for Euler/Navier-Stokes level of physics while meeting the vitally important robustness and efficiency criteria for rapid turnaround of the design system. The target time criteria for optimizations using the 3DOPT system is 1 day for Euler and 3 days for Navier-Stokes on a Cray C-90 class computer for a wing/body configuration capable of being resolved with a single block grid. This requires approximately a 1.5 hour turnaround of a single Navier-Stokes solution on a Cray C-90. CFL3D and TLNS3D are codes that meet or approach the timing goals. Table 1 presents timing and memory comparisons for the two codes. Multigrid is a feature of each code that contributes to efficient solutions. Both codes also have a full range of boundary conditions and turbulence models, but CFL3D has overlapped grid (Chimera) and moving mesh capability. TLNS3D's solver is Runge-Kutta based while CFL3D uses a diagonalized approximate factorization. CFL3D has a lower memory requirement and requires less solution time per step, but efficiency must necessarily include the number of steps required for convergence, and TLNS3D proved better in that respect.
|
|
Y-MP microsec per grid point per iteration | Memory locations per grid point * | Y-MP time, hours** |
| CFL3D | 26 | 45 | 0.9 |
| TLNS3D | 45 | 65 | 1.6 |
As a result of the trade study, TLNS3D was chosen as having a slight edge over CFL3D for the initial version of 3DOPT. However, the modular approach to integrating the flow solver into 3DOPT could easily accommodate a different code. Future versions of 3DOPT would benefit from a code capable of overset meshes, a powerful method for accommodating complex geometry, especially when automation is desired. Less mature, but promising technology, such as that represented in unstructured grid and Cartesian based codes, could also be incorporated in the 3DOPT system. These capabilities provide a growth path for 3DOPT that is limited only by the maturity of the solver and by its applicability to the optimization applications addressed by the system.
Approximate Modeling
Response surfaces or surrogate models are approximations to more detailed and expensive computer analysis models. These models may be least squares models, or in the case of the 3DOPT system, models that interpolate. In either case they are constructed to approximate the exact objective function surface by sampling design space at a carefully selected number of parameter value settings, or sample points. The surrogate model is constructed by running the expensive analysis code at the sample points and then fitting the surface. Surrogate models provide the designer with insight into the behavior of a complex optimization problem by allowing the user to identify and eliminate variables that have little effect. The function optimizer then interrogates the surrogate model for objective function values rather than run an expensive analysis code thereby reducing the total number of function evaluations for the optimization process.
3DOPT contains the suite of software known as DACEPAC. Design and Analysis of Computer Experiments (DACE, Ref 11) is a method of exploring the relationship between a computer simulation’s input variables and its output values. This exploration has three elements. First, the establishment of a judicious choice of combinations of settings of the input variables at which to run the simulation and obtain output, or response, values. Second, creation of a model of the output as a function of the input variables. In this document we call this surrogate model an interpolating response surface (IRS). Third, interrogation of the model and analysis of the experiment in terms of the individual and pairwise effects of the variables on the IRS and in terms of the importance of these effects.
3DOPT implementation of DACE provides a systematic and automated way to cover the input space when sampling output. Distributions of sampling points throughout the design space can be obtained by one of two methods. First, optimal experimental designs based on a probabilistic interpretation of a model fit are available for cases with 15 to 20 design variables. The other space filling design capability is orthogonal arrays in the sense of Owen (Ref 12). The resulting kriging model (IRS) interpolates the responses into a fit based on an assumption of an underlying Gaussian process. This model provides a global look at the input-output relationship. DACE analysis of this IRS model can then be used to find good regions of input space for further exploration or optimization, gain insight into regions with candidate optima, reduce the number of input variables, and summarize the results of a DACE experiment through graphical presentation.
Multipoint Design Optimization
The choice of a numerical optimization method depends, to a great extent, on the characteristics of the problem under consideration. Aerodynamic design problems can exhibit several features that challenge the optimizer, including expensive function evaluations, a large number of design variables and multiple local optimum points. In addition, the possibility of non-unique as well as discontinuous flow solutions with random numerical error must be considered. A growing list of optimization methods available includes calculus-based methods, random directed methods such as genetic and simulated annealing algorithms, neural networks and expert systems. From this list we select two, calculus-based and genetic algorithms, for further discussion.
Calculus-based numerical optimization methods, including the various gradient methods (Ref 13), use design variable sensitivity information to form local models of the objective function surface. The local models are used, in a repeated iteration, to find a point in design space where the sensitivity is zero, a necessary but not sufficient condition for a local minimum. Calculus-based methods are efficient and reliable means for finding optimum points where the objective function surface is known to be smooth, i.e., is continuous and has continuous first, and with some methods, second derivatives. With repeated application from different starting points calculus-based methods can be used to locate the global optimum point in cases where a small number of local minimum points occur. The smoothness requirement and the need for sensitivities are disadvantages for calculus based methods unless additional means are provided to alleviate these shortcomings. If methods are provided for finding the vicinity of a global optimum as well as ensuring smoothness, the calculus-based methods are viable candidates for finishing an optimization problem.
Guided random search numerical optimization methods are global optimizers that usually exploit or mimic principles observed in natural systems. The genetic algorithm (Ref 14) is one of these methods that have found general application.
Genetic algorithms employ a bit-string representation of a population of initially randomly selected points in design space and the principles of parental selection, genetic crossover, mutation and survival of the fittest to drive the population toward a global optimum. Genetic algorithms have been used in a broad range of optimization applications including aircraft preliminary design, structural design, curve fitting, financial resource allocation, scheduling, and neural network training. Genetic algorithms are a tool of Artificial Intelligence in that knowledge of the design space is acquired and exploited to aid in the optimization process.
The genetic algorithm is easy to implement, is reasonably robust, and does not impose smoothness requirements on the objective function. This method is a global optimizer. However, the genetic algorithm is not without it’s drawbacks. It generally requires a large number of function evaluations that scales roughly with the square of the number of design variables. Constraints are usually handled by augmenting the objective function with weighted penalties.
For implementation into the 3DOPT system we selected a combination of methods interfaced to approximate models of the design space. The first method is a hybrid genetic/gradient method. In this approach the genetic algorithm identifies the local region where the global optimum is located. The calculus-based method is then used to find, starting from the most promising point found by the genetic algorithm, the location of the global optimum point. We are using a six-bit binary integer representation of each design variable with a cyclic Gray code method (Ref 15) of decoding. A uniform crossover operation is initiated for 90% of a given generation. Within this subset 50% of the bits are exchanged. Mutation through bit flipping is initiated on average for one bit per child.
To complement the hybrid genetic/gradient optimization method, a repeated application of calculus based methods approach was also integrated into the 3DOPT system. Both methods make use of NPSOL (Ref 9), a sequential quadratic programming (SQP) method (Ref 13), to provide a local, calculus based design space search. The repeated application approach is based on random sampling of the objective function. Independent NPSOL applications are initiated at each starting point selected. Selection criteria are based on the value of the objective function and distance from previous points. The collection of results from each of the local searches is sorted to identify the search producing the greatest improvement in the objective function, thus identifying the global optimum.
Implementation of a multipoint objective function is accomplished with the use of weighted averages of an objective function from each design point. The current implementation limits the formulation of objective functions to lift, drag or pitching moment. Future enhancements will extend this to arbitrary combinations of integrated force and moments or extrema of local surface characteristics such as pressure coefficient or Mach number. Enforcement of aerodynamic constraints with the hybrid genetic/gradient method is accomplished through the formation of an augmented objective function modified by adding a penalty for constraint violation. The repeated NPSOL approach makes use of direct interrogation of surrogate models representing aerodynamic constraint values. Both approaches use a penalty function implementation to maintain geometric constraints.
Control Scripts and GUI
Control of the 3DOPT-system process and communication between modules is maintained by a collection of UNIX C shell scripts. Transfer of user input information is achieved through a master namelist file and parser utilities that extract or modify namelist parameter definitions as needed through out the 3DOPT process. This namelist file also acts as the conduit between the Graphical User Interface (GUI) and these control-scripts. This provides for either an interactive execution of the system or a batch submittal. During interactive execution the user inputs the required data via the GUI, which edits the namelist-file accordingly and directs the conduct of the optimization.
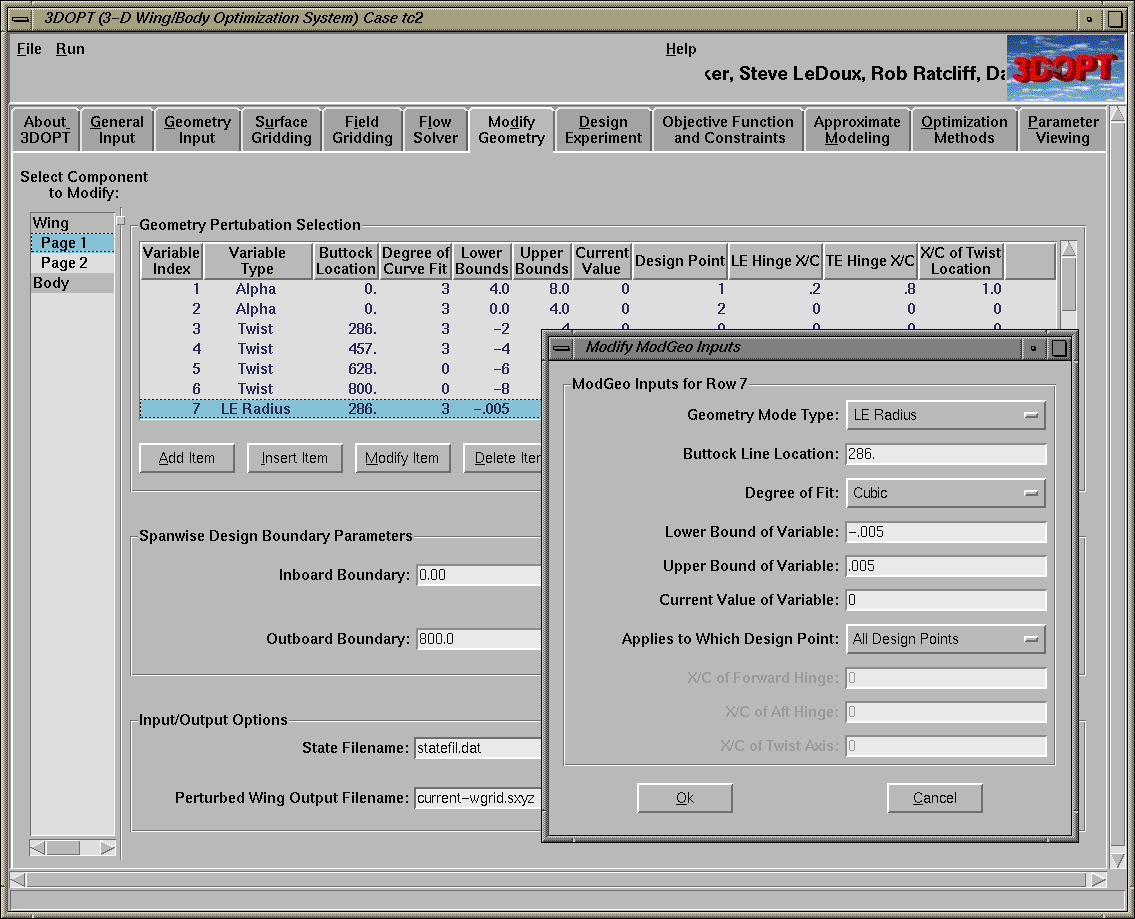
Currently, the 3DOPT system contains over 200 input variables in the namelist control file. As the system matures, the number of inputs could very well grow to an unmanageable number, if the user was required to manually edit the namelist control file. In order to alleviate this burden, the graphic interface was developed to allow the user to control the entire optimization process in an intuitive manner. There were several requirements of the GUI that led to a decision to use the public domain GUI scripting language developed by John Ousterhout at Sun Labs called TCL/TK (Ref 16) and the sophisticated Windows 95 like widget set developed by Ioi Lam at XPI called Tix (Ref 17), rather than the traditional C based Motif approach. By using this GUI scripting language, portability issues associated with the traditional C/Motif based GUI's have been avoided, as TCL/TK/Tix uses an interpreter, which has been compiled on most Unix platforms, as well as Windows 95 and NT. Once the correct version of the interpreter is available, the 3DOPT GUI script will run identically on all platforms except for any platform dependent system calls (such as calls to Unix scripts.). A sample 3DOPT GUI page, displaying the geometry modification inputs, is illustrated in Figure 4.
Two test cases were conducted to demonstrate system capabilities and operation. Only one will be discussed here. This case was formulated as a single point, Mach 0.9, transonic drag minimization task with lift and pitching moment constraints. Navier-Stokes level physics were used to compute aerodynamic characteristics. The geometry consisted of a 60o swept (leading edge) delta wing with an unswept trailing edge and a sharp tip. A total of 29 design variables were used, comprised of twist, camber, maximum thickness location, maximum camber location and vehicle angle-of-attack, as shown in Table 2 below. The constraints applied to this test case are displayed in Table 3. Selection of these constraints was done for demonstration purposes. The aerodynamic constraints
|
|
|
|
| Twist |
|
|
| Camber form |
|
|
| Max t/c location |
|
|
| Max camber location |
|
|
| Alpha |
|
|
| Total |
|
|
|
|
|
|
| Lift Coefficient | .599 | .601 |
| Pitching Moment
(Kept same as seed) |
-.044 | -.034 |
| Max t/c location (x/c) | .2 | .8 |
| Leading edge radius | .001 | 16 |
| Trailing edge closure | 26 deg | 46 deg |
| Chordwise Curvature | -1.0 | 1.0 |
| Spanwise Curvature | -0.167 | 0.167 |
were simply constraining the design targets to the original baseline pitching moment values. In a similar vein, curvature constraints were added to represent imposition of manufacturing constraints in a generic sense but not a specific manufacturing process.
The results of the design space search are summarized in Table 4 along with values from baseline and verification runs. In Table 4, ‘model optimum’ refers the result obtained from the interpolated response surface model at the optimal set of design variables. Verification runs, on the other hand, refer to post-optimal analysis of the optimal geometry with TLNS3D. Discrepancies observed between model predictions and verification runs are indicative of the level of error present in the surrogate model of the design space. This presents the designer with several choices for subsequent action. The surrogate modeling process could be iterated following some logic for data enrichment to reduce modeling errors. Alternatively, the design process could switch to a local, direct driven optimization procedure under the assumption that the region of best design has been located. Or the process could simply be terminated accepting the improvements derived to this point.
|
|
|
|
|
|
| Baseline | 12.00 |
|
|
|
| Model optimum | 10.67 |
|
|
|
| Verification run 1 | 10.67 |
|
|
|
| Verification run 2 | 12.00 |
|
|
|
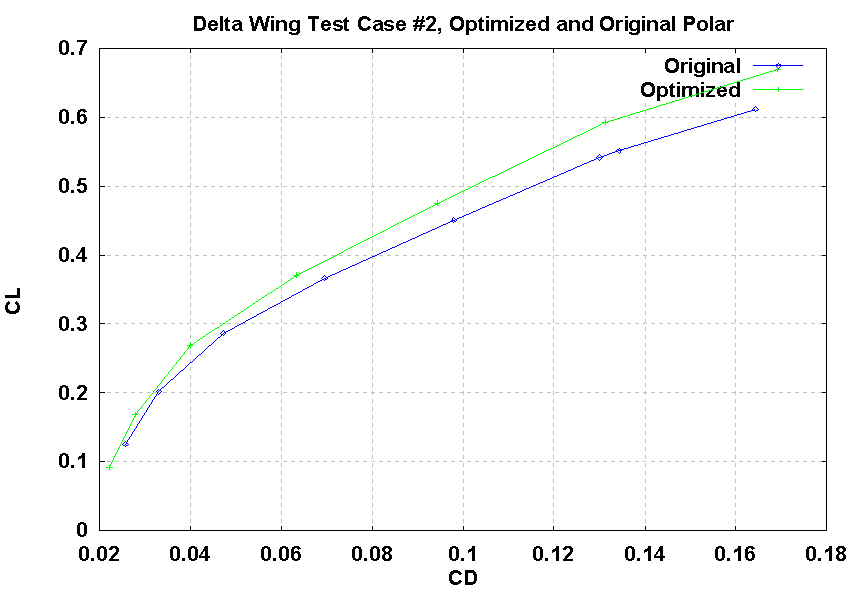
From the perspective of the current results, terminating the design process after a single IRS model construction iteration would produce performance improvements as indicated in Figure 5. Based on the drag polar shown in the figure, approximately a 15% reduction in drag at the design lift coefficient of 0.6 was achieved. As verification run 2 from Table 4 indicates, this level of improvement was obtained while meeting imposed pitching moment constraints. Furthermore, analysis of the optimal geometry indicated that all imposed geometric constraints were also met.
The 3DOPT software system represents a major step forward in the development of design optimization capability. It is a unique combination of higher order geometric functionality with Navier-Stokes level flow analysis, approximate modeling techniques and robust numerical optimization schemes in an automated framework. This system provides a means to achieve increased aerodynamic performance while controlling computational resources during a design cycle. Flexibility of use and potential for growth has been provided through a modular system design that will run on high performance computers as well as engineering workstations.
3DOPT was developed for the Air Force Research Laboratory
(formerly Wright Laboratory), Wright-Patterson AFB, Ohio, under the 3-Dimensional
Design Optimization, Contract Number F33615-94-C-3001. The work was performed
by the Boeing Company, Information, Space & Defense Systems. Dr. Don
Kinsey, Captain. Gregg Sharp, Captain. Eric Fick and Mr. Howard Emsley
were the USAF Project Engineers. Dr. Fritz Roetman was the Boeing Program
Manager and Dr. William Herling was the Principal Investigator. In addition
to the authors, program development was completed by Mr. Gordon Blom and
Dr. Andrew Booker. Contributions from Captains Sharp and Fick are gratefully
acknowledged. Their testing and feedback during the development of this
system was a key component to the successful completion of 3DOPT. Likewise,
Mr. Philip Kraushar’s timely improvements to the DTNURBS geometry library
was an essential contribution to the efficient operation of 3DOPT geometry
processes. Finally, acknowledgment is given to NASA for the technology
contributions to several of the system modules. These include TWING, TLNS3D,
HYPGEN and WINGDES.